https://www.acmicpc.net/problem/11657
알고리즘 분류 : 그래프 이론, 최단 경로, 벨만–포드
❓문제
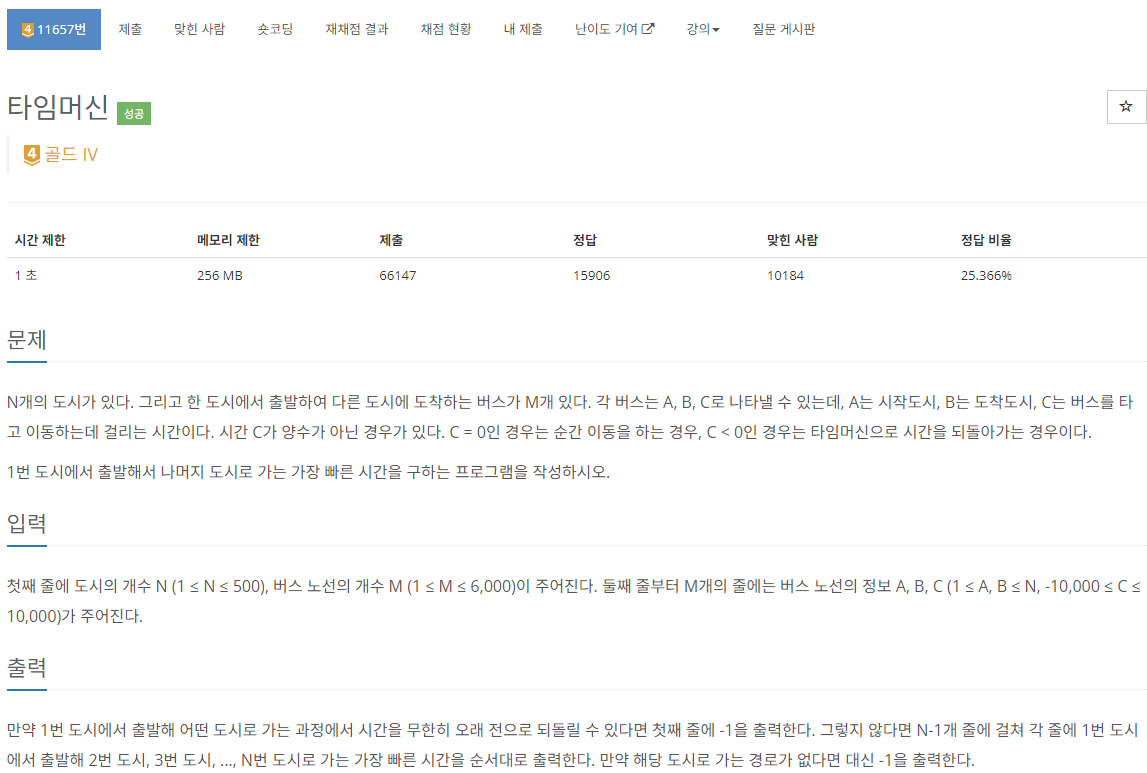
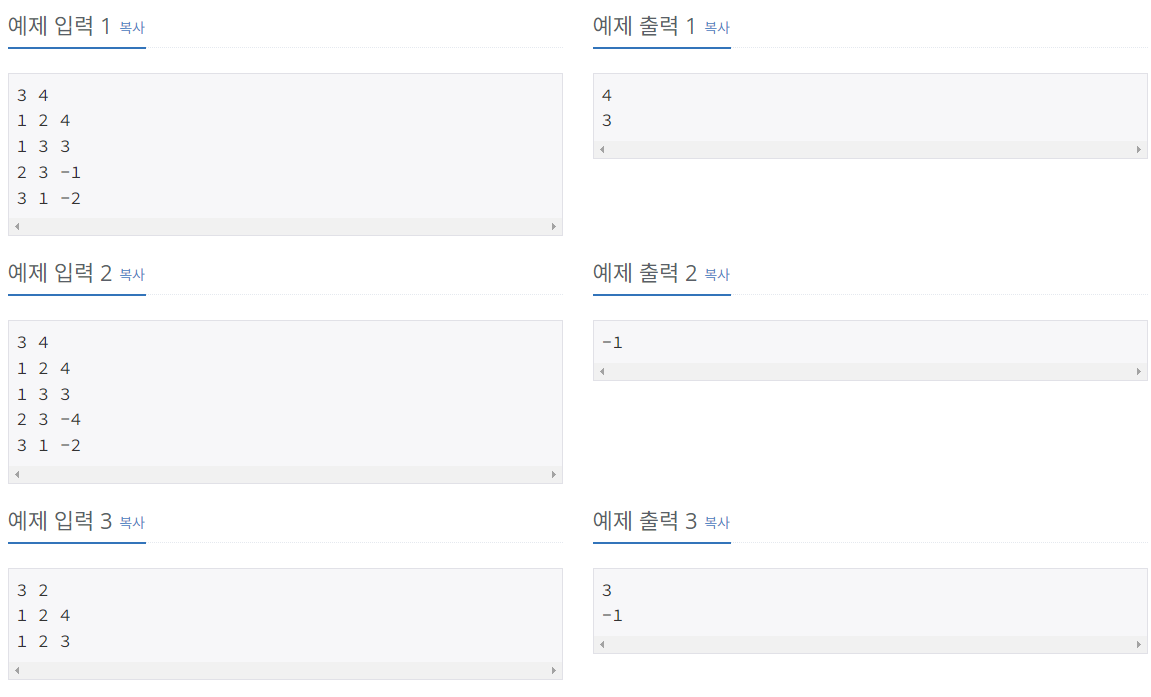
🔅해석
1. 거리 초기화
시작 정점의 거리를 0으로 설정하고, 나머지 모든 정점의 거리를 무한대로 설정한다.

2. 거리 갱신
모든 간선에 대해 V-1번 반복해서 간선의 시작 정점에서 도착 정점으로 가는 경로가 현재 알려진 경로보다 짧다면, 그 경로를 갱신한다.

dist[from] > dist[to] + edge.cost 이므로 dist 업데이트를 한다.

dist[from] > dist[to] + edge.cost 이므로 dist 업데이트를 한다.

dist[from] == dist[to] + edge.cost 이므로 dist 업데이트 되지 않는다.

dist[from] < dist[to] + edge.cost 이므로 dist 업데이트 되지 않는다.
이렇게 (V - 1) * E 번 반복하여 거리 계산을 한다.
3. 음수 사이클 검출
마지막으로 모든 간선에 대해 추가로 한 번 더 거리 갱신을 한다. 이 과정에서 최단 거리 갱신이 되면, 음수 사이클이 존재한다고 판단할 수 있다.
해당 테스트케이스의 경우, 음수 사이클이 존재하지 않는다.
⭕정답 코드
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
static class Edge {
int from;
int to;
int cost;
public Edge(int from, int to, int cost) {
this.from = from;
this.to = to;
this.cost = cost;
}
}
static long[] dist;
static ArrayList<Edge> adjList;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
dist = new long[N + 1];
adjList = new ArrayList<>();
int A, B, C;
for (int m = 0; m < M; m++) {
st = new StringTokenizer(br.readLine());
A = Integer.parseInt(st.nextToken());
B = Integer.parseInt(st.nextToken());
C = Integer.parseInt(st.nextToken());
adjList.add(new Edge(A, B, C));
}
StringBuilder sb = new StringBuilder();
if (bellmanFordMoore(N, 1)) {
sb.append("-1\n");
} else {
for (int i = 2; i <= N; i++) {
if (dist[i] == Long.MAX_VALUE) {
sb.append("-1\n");
} else {
sb.append(dist[i]).append("\n");
}
}
}
bw.write(sb.toString());
bw.flush();
bw.close();
br.close();
}
static boolean bellmanFordMoore(int V, int start) {
Arrays.fill(dist, Long.MAX_VALUE);
dist[start] = 0;
// V-1번 E개의 모든 간선 확인
for (int i = 0; i < V - 1; i++) {
for (Edge edge : adjList) {
// 간선의 시작점이 아직 탐색 불가면 continue
if (dist[edge.from] == Long.MAX_VALUE) {
continue;
}
// 최단거리 갱신
if (dist[edge.to] > dist[edge.from] + edge.cost) {
dist[edge.to] = dist[edge.from] + edge.cost;
}
}
}
boolean isNegativeCycle = false;
// V번째 E개의 모든 간선을 확인해서 갱신되는 구간이 있으면 음의 사이클이 존재하는 것
for (Edge edge : adjList) {
if (dist[edge.from] == Long.MAX_VALUE) {
continue;
}
if (dist[edge.to] > dist[edge.from] + edge.cost) {
isNegativeCycle = true;
break;
}
}
return isNegativeCycle;
}
}
❗결과

'코딩테스트 > 백준' 카테고리의 다른 글
| [코테] 백준 23968번 : 알고리즘 수업 - 버블 정렬 1 (java) (0) | 2024.11.01 |
|---|---|
| [코테] 백준 2458번 : 키 순서 (java) (0) | 2024.08.16 |
| [코테] 백준 1753번 : 최단경로 (java) (0) | 2024.08.16 |
| [코테] 백준 11438번 : LCA 2 (java) (0) | 2024.08.16 |
| [코테] 백준 1922번 : 네트워크 연결 (java) (0) | 2024.08.15 |
https://www.acmicpc.net/problem/11657
알고리즘 분류 : 그래프 이론, 최단 경로, 벨만–포드
❓문제


🔅해석
1. 거리 초기화
시작 정점의 거리를 0으로 설정하고, 나머지 모든 정점의 거리를 무한대로 설정한다.

2. 거리 갱신
모든 간선에 대해 V-1번 반복해서 간선의 시작 정점에서 도착 정점으로 가는 경로가 현재 알려진 경로보다 짧다면, 그 경로를 갱신한다.

dist[from] > dist[to] + edge.cost 이므로 dist 업데이트를 한다.

dist[from] > dist[to] + edge.cost 이므로 dist 업데이트를 한다.

dist[from] == dist[to] + edge.cost 이므로 dist 업데이트 되지 않는다.

dist[from] < dist[to] + edge.cost 이므로 dist 업데이트 되지 않는다.
이렇게 (V - 1) * E 번 반복하여 거리 계산을 한다.
3. 음수 사이클 검출
마지막으로 모든 간선에 대해 추가로 한 번 더 거리 갱신을 한다. 이 과정에서 최단 거리 갱신이 되면, 음수 사이클이 존재한다고 판단할 수 있다.
해당 테스트케이스의 경우, 음수 사이클이 존재하지 않는다.
⭕정답 코드
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
static class Edge {
int from;
int to;
int cost;
public Edge(int from, int to, int cost) {
this.from = from;
this.to = to;
this.cost = cost;
}
}
static long[] dist;
static ArrayList<Edge> adjList;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
dist = new long[N + 1];
adjList = new ArrayList<>();
int A, B, C;
for (int m = 0; m < M; m++) {
st = new StringTokenizer(br.readLine());
A = Integer.parseInt(st.nextToken());
B = Integer.parseInt(st.nextToken());
C = Integer.parseInt(st.nextToken());
adjList.add(new Edge(A, B, C));
}
StringBuilder sb = new StringBuilder();
if (bellmanFordMoore(N, 1)) {
sb.append("-1\n");
} else {
for (int i = 2; i <= N; i++) {
if (dist[i] == Long.MAX_VALUE) {
sb.append("-1\n");
} else {
sb.append(dist[i]).append("\n");
}
}
}
bw.write(sb.toString());
bw.flush();
bw.close();
br.close();
}
static boolean bellmanFordMoore(int V, int start) {
Arrays.fill(dist, Long.MAX_VALUE);
dist[start] = 0;
// V-1번 E개의 모든 간선 확인
for (int i = 0; i < V - 1; i++) {
for (Edge edge : adjList) {
// 간선의 시작점이 아직 탐색 불가면 continue
if (dist[edge.from] == Long.MAX_VALUE) {
continue;
}
// 최단거리 갱신
if (dist[edge.to] > dist[edge.from] + edge.cost) {
dist[edge.to] = dist[edge.from] + edge.cost;
}
}
}
boolean isNegativeCycle = false;
// V번째 E개의 모든 간선을 확인해서 갱신되는 구간이 있으면 음의 사이클이 존재하는 것
for (Edge edge : adjList) {
if (dist[edge.from] == Long.MAX_VALUE) {
continue;
}
if (dist[edge.to] > dist[edge.from] + edge.cost) {
isNegativeCycle = true;
break;
}
}
return isNegativeCycle;
}
}
❗결과

'코딩테스트 > 백준' 카테고리의 다른 글
| [코테] 백준 23968번 : 알고리즘 수업 - 버블 정렬 1 (java) (0) | 2024.11.01 |
|---|---|
| [코테] 백준 2458번 : 키 순서 (java) (0) | 2024.08.16 |
| [코테] 백준 1753번 : 최단경로 (java) (0) | 2024.08.16 |
| [코테] 백준 11438번 : LCA 2 (java) (0) | 2024.08.16 |
| [코테] 백준 1922번 : 네트워크 연결 (java) (0) | 2024.08.15 |
