https://www.acmicpc.net/problem/1922
알고리즘 분류 : 그래프 이론, 최소 스패닝 트리
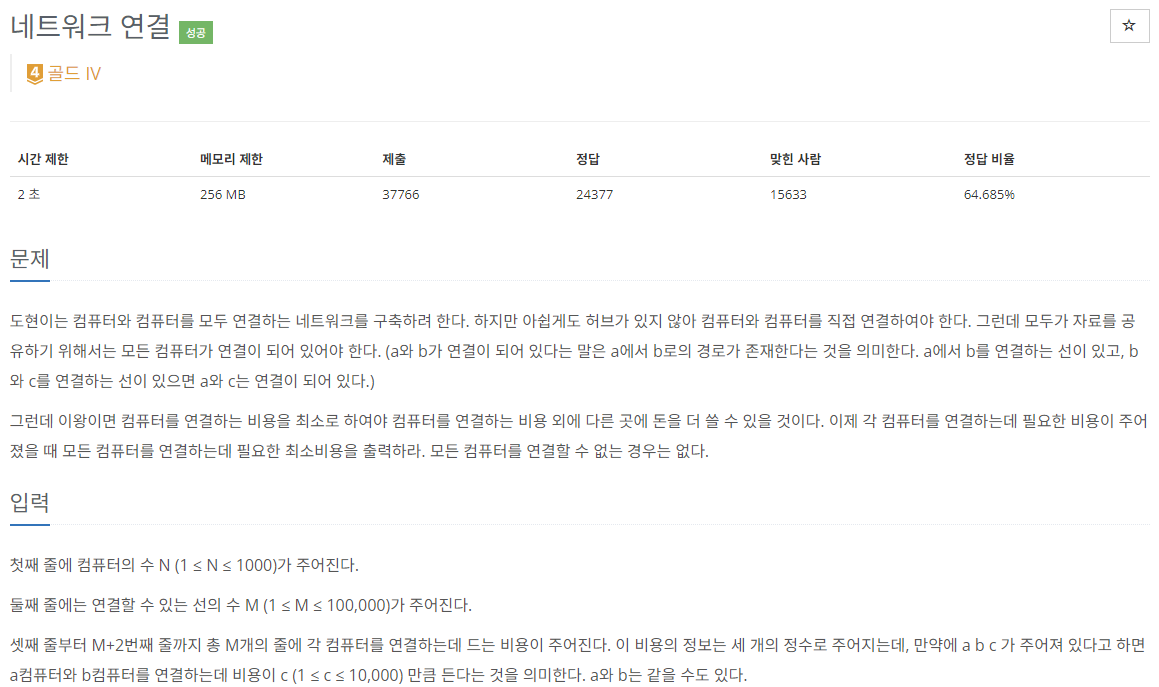
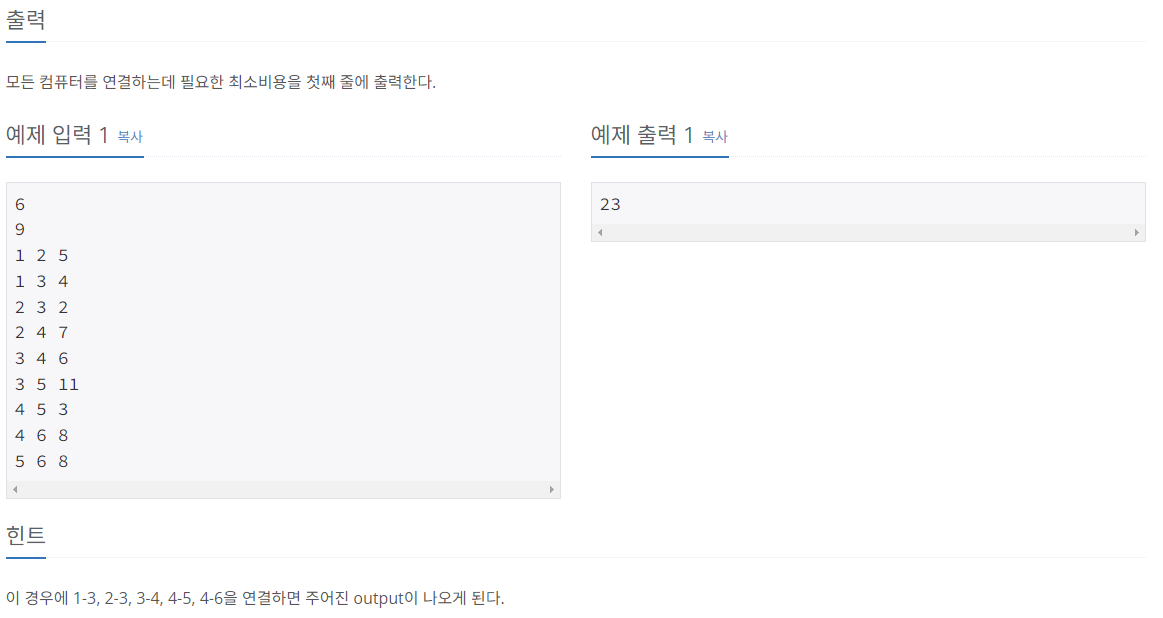
❓문제
🔅해석
컴퓨터 == 정점
선 == 간선
모든 컴퓨터(정점)를 연결하여 최소의 비용(가중치)을 얻기 위해 MST를 구현한다.
MST를 구하기 위한 알고리즘에는 크루스칼, 프림이 있는데 크루스칼로 풀이해본다.
// input
6
9
1 2 5
1 3 4
2 3 2
2 4 7
3 4 6
3 5 11
4 5 3
4 6 8
5 6 8
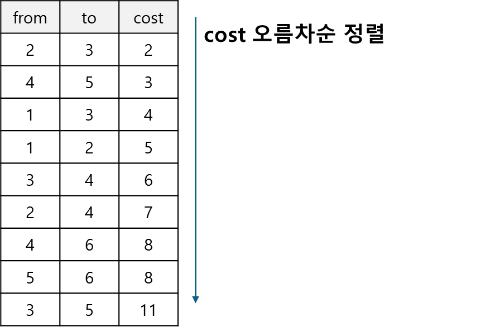
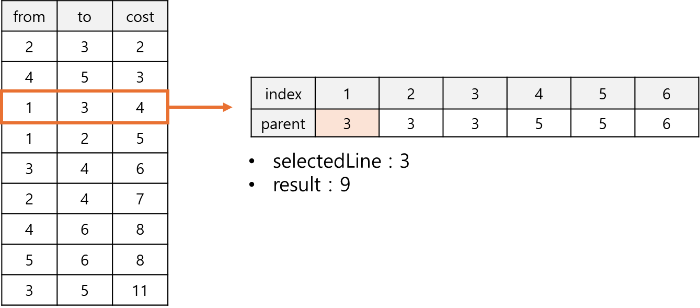
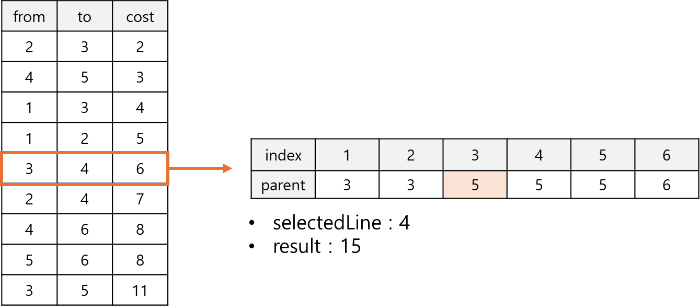
1. 간선 정렬
그래프의 모든 간선을 가중치 기준으로 오름차순 정렬한다.
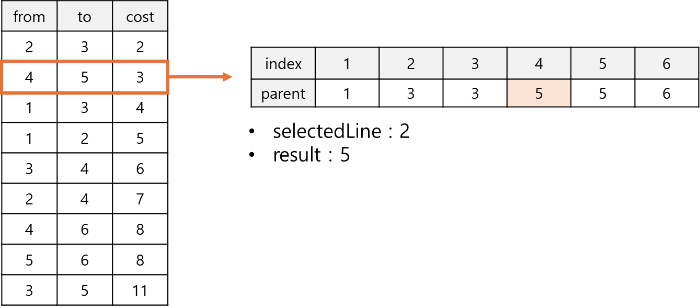
2. 간선 선택
정렬된 간선 리스트에서 순차적으로 간선을 선택한다. 이때, 선택된 간선이 사이클을 형성하지 않는다면 해당 간선을 최소 신장 트리에 추가한다.
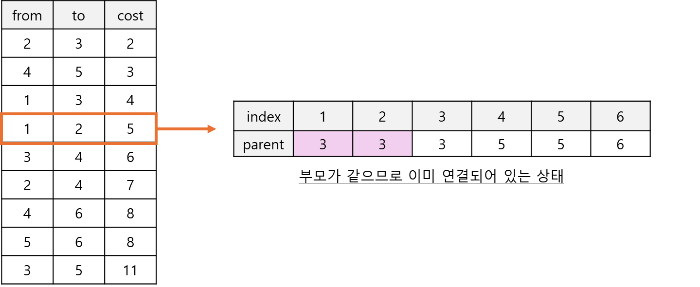
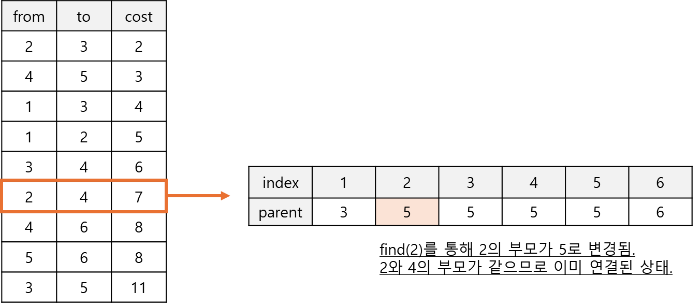
3. 사이클 검증
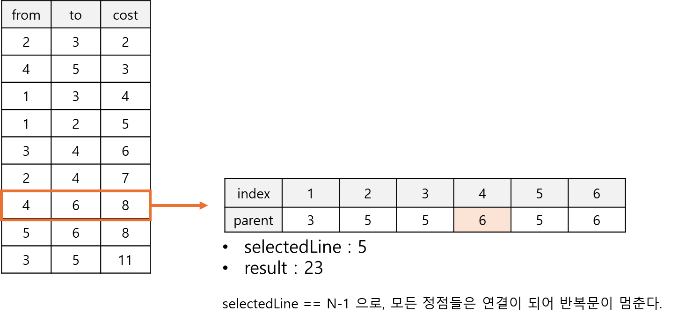
사이클이 형성되는지 확인하기 위해서 유니온-파인드(Union-Find) 자료 구조를 사용한다. 두 정점이 이미 같은 집합(연결된 트리)에 속해 있다면, 그 간선을 선택하지 않는다.

2와 3의 부모가 일치하지 않아, 사이클을 형성하지않는다.0
4. 반복
모든 정점이 연결될 때까지(즉, 간선의 수가 정점 수 - 1이 될 때까지) 이 과정을 반복한다.
⭕정답 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.Comparator;
import java.util.StringTokenizer;
public class Main {
static int N, M;
static Edge[] edge;
static int[] parent;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
N = Integer.parseInt(br.readLine());
M = Integer.parseInt(br.readLine());
edge = new Edge[M];
parent = new int[N + 1];
parentInit();
int a, b, c;
for (int m = 0; m < M; m++) {
st = new StringTokenizer(br.readLine());
a = Integer.parseInt(st.nextToken());
b = Integer.parseInt(st.nextToken());
c = Integer.parseInt(st.nextToken());
edge[m] = new Edge(a, b, c);
}
System.out.println(kruskal());
}
private static void parentInit() {
for (int n = 1; n <= N; n++) {
parent[n] = n;
}
}
private static int kruskal() {
int selectedLine = 0;
int result = 0;
// cost 오름차순 정렬
Arrays.sort(edge, Comparator.comparing(Edge::getCost));
union(edge[0].from, edge[0].to);
selectedLine++;
result += edge[0].cost;
int from, to, cost;
int aRoot, bRoot;
for (int m = 1; m < M; m++) {
from = edge[m].from;
to = edge[m].to;
cost = edge[m].cost;
aRoot = find(from);
bRoot = find(to);
// 같은 set 안에 없다면 연결되어 있지 않은 상태
if (aRoot != bRoot) {
result += cost;
union(from, to);
selectedLine++;
}
if (selectedLine >= N-1) break;
}
return result;
}
private static void union(int a, int b) {
int aRoot = find(a);
int bRoot = find(b);
if (aRoot != bRoot) {
parent[aRoot] = bRoot;
}
}
private static int find(int a) {
if (parent[a] == a) return a;
return parent[a] = find(parent[a]);
}
}
class Edge implements Comparable<Edge> {
int from;
int to;
int cost;
public Edge(int from, int to, int cost) {
super();
this.from = from;
this.to = to;
this.cost = cost;
}
public int getFrom() {
return from;
}
public int getTo() {
return to;
}
public int getCost() {
return cost;
}
@Override
public int compareTo(Edge o1) {
return o1.cost - cost;
}
}
❗결과

'코딩테스트 > 백준' 카테고리의 다른 글
| [코테] 백준 1753번 : 최단경로 (java) (0) | 2024.08.16 |
|---|---|
| [코테] 백준 11438번 : LCA 2 (java) (0) | 2024.08.16 |
| [코테] 백준 2252번 : 줄 세우기 (java) (0) | 2024.08.15 |
| [코테] 백준 3830번 : 교수님은 기다리지 않는다 (java) (0) | 2024.08.15 |
| [코테] 백준 1717번 : 집합의 표현 (java) (0) | 2024.08.15 |
https://www.acmicpc.net/problem/1922
알고리즘 분류 : 그래프 이론, 최소 스패닝 트리
❓문제


🔅해석
컴퓨터 == 정점
선 == 간선
모든 컴퓨터(정점)를 연결하여 최소의 비용(가중치)을 얻기 위해 MST를 구현한다.
MST를 구하기 위한 알고리즘에는 크루스칼, 프림이 있는데 크루스칼로 풀이해본다.
// input
6
9
1 2 5
1 3 4
2 3 2
2 4 7
3 4 6
3 5 11
4 5 3
4 6 8
5 6 8
1. 간선 정렬
그래프의 모든 간선을 가중치 기준으로 오름차순 정렬한다.

2. 간선 선택
정렬된 간선 리스트에서 순차적으로 간선을 선택한다. 이때, 선택된 간선이 사이클을 형성하지 않는다면 해당 간선을 최소 신장 트리에 추가한다.
3. 사이클 검증
사이클이 형성되는지 확인하기 위해서 유니온-파인드(Union-Find) 자료 구조를 사용한다. 두 정점이 이미 같은 집합(연결된 트리)에 속해 있다면, 그 간선을 선택하지 않는다.

2와 3의 부모가 일치하지 않아, 사이클을 형성하지않는다.0
4. 반복
모든 정점이 연결될 때까지(즉, 간선의 수가 정점 수 - 1이 될 때까지) 이 과정을 반복한다.






⭕정답 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.Comparator;
import java.util.StringTokenizer;
public class Main {
static int N, M;
static Edge[] edge;
static int[] parent;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
N = Integer.parseInt(br.readLine());
M = Integer.parseInt(br.readLine());
edge = new Edge[M];
parent = new int[N + 1];
parentInit();
int a, b, c;
for (int m = 0; m < M; m++) {
st = new StringTokenizer(br.readLine());
a = Integer.parseInt(st.nextToken());
b = Integer.parseInt(st.nextToken());
c = Integer.parseInt(st.nextToken());
edge[m] = new Edge(a, b, c);
}
System.out.println(kruskal());
}
private static void parentInit() {
for (int n = 1; n <= N; n++) {
parent[n] = n;
}
}
private static int kruskal() {
int selectedLine = 0;
int result = 0;
// cost 오름차순 정렬
Arrays.sort(edge, Comparator.comparing(Edge::getCost));
union(edge[0].from, edge[0].to);
selectedLine++;
result += edge[0].cost;
int from, to, cost;
int aRoot, bRoot;
for (int m = 1; m < M; m++) {
from = edge[m].from;
to = edge[m].to;
cost = edge[m].cost;
aRoot = find(from);
bRoot = find(to);
// 같은 set 안에 없다면 연결되어 있지 않은 상태
if (aRoot != bRoot) {
result += cost;
union(from, to);
selectedLine++;
}
if (selectedLine >= N-1) break;
}
return result;
}
private static void union(int a, int b) {
int aRoot = find(a);
int bRoot = find(b);
if (aRoot != bRoot) {
parent[aRoot] = bRoot;
}
}
private static int find(int a) {
if (parent[a] == a) return a;
return parent[a] = find(parent[a]);
}
}
class Edge implements Comparable<Edge> {
int from;
int to;
int cost;
public Edge(int from, int to, int cost) {
super();
this.from = from;
this.to = to;
this.cost = cost;
}
public int getFrom() {
return from;
}
public int getTo() {
return to;
}
public int getCost() {
return cost;
}
@Override
public int compareTo(Edge o1) {
return o1.cost - cost;
}
}
❗결과

'코딩테스트 > 백준' 카테고리의 다른 글
| [코테] 백준 1753번 : 최단경로 (java) (0) | 2024.08.16 |
|---|---|
| [코테] 백준 11438번 : LCA 2 (java) (0) | 2024.08.16 |
| [코테] 백준 2252번 : 줄 세우기 (java) (0) | 2024.08.15 |
| [코테] 백준 3830번 : 교수님은 기다리지 않는다 (java) (0) | 2024.08.15 |
| [코테] 백준 1717번 : 집합의 표현 (java) (0) | 2024.08.15 |
