다익스트라 알고리즘 (Dijkstra's Algorithm)
- 음이 아닌 가중 그래프에서의 단일 쌍, 단일 출발, 단일 도착 최단 경로 문제
- 시작점이 있고, 모든 노드로 최단 거리를 구할 때
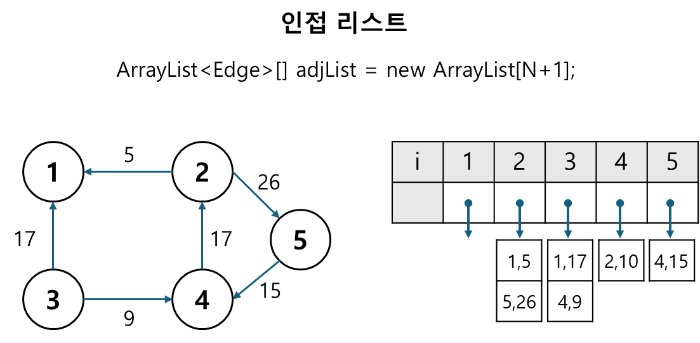
- 인접 리스트 사용
- PQ로 최소 cost 뽑으면서 정점을 방문하여 최단 거리 갱신
- 음의 간선이 없으므로 각 노드에 최초 방문 시 최단 거리를 확정한다. (방문 체크 필요)
동작 원리
- 시작 정점 설정
- 시작 정점을 선택하고, 이 정점에서 다른 모든 정점으로의 최단 거리를 저장할 배열을 초기화한다. 시작 정점의 거리는 0으로 설정하고, 나머지 정점의 거리는 무한대로 설정한다.
- 방문하지 않은 정점 중 최단 거리 정점 선택한다.
- 인접한 정점들의 거리 갱신
- 선택한 정점의 인접한 정점들에 대해, 현재 정점을 거쳐 가는 것이 더 짧은 경로라면, 그 경로로 거리를 갱신한다.
- 모든 정점을 방문할 때까지 반복한다.
Node 클래스
정점의 번호와 해당 정점까지의 비용을 포함한다.
Comparable 인터페이스를 구현하여 우선순위 큐에서 최소 비용의 정점이 먼저 나오도록 한다.
static class Node implements Comparable<Node> {
int dest;
int cost;
public Node(int dest, int cost) {
this.dest = dest;
this.cost = cost;
}
@Override
public int compareTo(Node o) {
return Integer.compare(this.cost, o.cost);
}
}
코드 구현
static void dijkstra(int start) {
PriorityQueue<Node> pq = new PriorityQueue<>();
Arrays.fill(dist, Integer.MAX_VALUE);
dist[start] = 0;
// 시작점: 1번 노드
pq.offer(new Node(start, 0));
while (!pq.isEmpty()) {
Node current = pq.poll();
// 목적지 노드가 이미 방문했던 정점이면 다시 방문하지 않는다
// 첫번째 방문에서 최단거리가 결정되기 때문
if (visited[current.dest]) {
continue;
}
// 방문처리
visited[current.dest] = true;
for (Node next : adjList[current.dest]) {
if (dist[next.dest] > next.cost + current.cost) {
dist[next.dest] = next.cost + current.cost;
pq.offer(new Node(next.dest, dist[next.dest]));
}
}
}
}
예제 문제
백준 1753번 : 최단경로
https://www.acmicpc.net/problem/1753
[코테] 백준 1753번 : 최단경로 (java)
https://www.acmicpc.net/problem/1753알고리즘 분류 : 그래프 이론, 데이크스트라, 최단 경로❓문제🔅해석음이 아닌 가중 그래프에서의 단일 쌍, 단일 출발, 단일 도착 최단 경로 문제에서는 다익스트라
steady-record.tistory.com
벨만-포드 알고리즘 (Bellman-Ford Algorithm)
- 가중 그래프에서의 단일 쌍, 단일 출발, 단일 도착 최단 경로 문제
- 음수의 간선을 포함 할 수 있다.
- 음수의 사이클이 존재할 수 있다.
- V-1번 탐색하여 최단 거리를 구하고 V번 구했을 때, 최단거리 갱신이 된다면, 음수의 사이클이 존재한다는 것이다.
- 케이스가 3000 ~ 5000
동작원리
- 거리 초기화
- 시작 정점의 거리를 0으로 설정하고, 나머지 모든 정점의 거리를 무한대로 설정한다.
- 거리 갱신
- 모든 간선에 대해 V-1번 반복해서 간선의 시작 정점에서 도착 정점으로 가는 경로가 현재 알려진 경로보다 짧다면, 그 경로를 갱신한다.
- 음수 사이클 검출
- 모든 간선에 대해 추가로 한 번 더 거리 갱신을 한다. 이 과정에서 최단 거리 갱신이 되면, 음수 사이클이 존재한다고 판단할 수 있다.
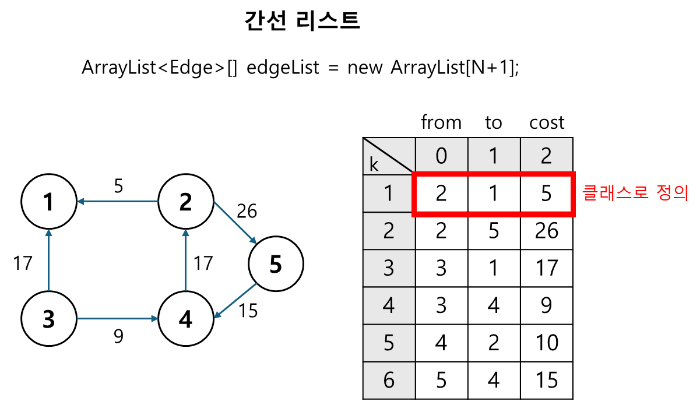
Edge 클래스
static class Edge{
int from;
int to;
int cost;
public Edge(int from, int to, int cost){
this.from = from;
this.to = to;
this.cost = cost;
}
}
코드 구현
static boolean bellmanFordMoore(int V, int start){
Arrays.fill(dist, Long.MAX_VALUE);
dist[start] = 0;
// V-1번 E개의 모든 간선 확인
for(int i=0; i<V-1; i++){
for(Edge edge : adjList){
// 간선의 시작점이 아직 탐색 불가면 continue
if(dist[edge.from] == Long.MAX_VALUE){
continue;
}
// 최단거리 갱신
if(dist[edge.to] > dist[edge.from] + edge.cost){
dist[edge.to] = dist[edge.from] + edge.cost;
}
}
}
boolean isNegativeCycle = false;
// V번째 E개의 모든 간선을 확인해서 갱신되는 구간이 있으면 음의 사이클이 존재하는 것
for(Edge edge : adjList){
if(dist[edge.from] == Long.MAX_VALUE){
continue;
}
if(dist[edge.to] > dist[edge.from] + edge.cost){
isNegativeCycle = true;
break;
}
}
return isNegativeCycle;
}
예제 문제
백준 11657번 : 타임 머신
https://www.acmicpc.net/problem/11657
문제 풀이
[코테] 백준 11657번 : 타임 머신 (java)
https://www.acmicpc.net/problem/11657알고리즘 분류 : 그래프 이론, 최단 경로, 벨만–포드❓문제 🔅해석 1. 거리 초기화 시작 정점의 거리를 0으로 설정하고, 나머지 모든 정점의 거리를 무한대
steady-record.tistory.com
플로이드-워셜 알고리즘 (Floyd-Warshall Algorithm)
- 전체 쌍 최단 경로 문제
- 케이스가 300 ~ 500
- 그래프에서 음수 가중치의 간선이 존재할 수 있지만, 음수 사이클(negative cycle)은 없어야 한다.
동작 원리
플로이드-워셜 알고리즘은 동적 프로그래밍(Dynamic Programming)을 기반으로 하며, 점진적으로 모든 정점 간의 최단 경로를 계산한다. 이 알고리즘의 핵심 아이디어는 "중간에 다른 정점을 거치는 경로가 직접 연결된 경로보다 더 짧을 수 있다"는 점이다.
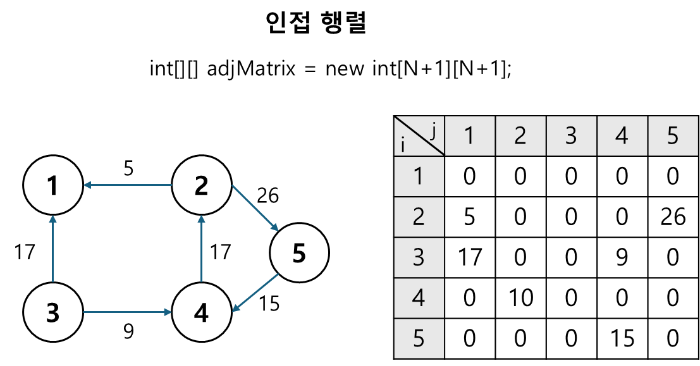
- 거리 초기화
- 그래프의 인접 행렬(Adjacency Matrix)로 초기화한다. 만약 두 정점 간에 직접 연결된 간선이 있다면 그 가중치로 초기화하고, 연결되어 있지 않다면 무한대(또는 매우 큰 값)로 설정한다. 자신에게 가는 거리는 0으로 설정한다.
- 동적 프로그래밍(DP) 적용
- 각 정점을 중간 정점으로 고려하여, 다른 모든 정점 쌍에 대해 최단 경로를 갱신한다. 즉, 정점 k를 중간 정점으로 사용하는 경우, i에서 j로 가는 경로가 i -> k -> j로 더 짧아질 수 있는지 확인하고, 그렇다면 경로를 갱신한다.
- 결과 출력 : 모든 정점 쌍 간의 최단 경로가 담긴 행렬을 출력합니다.
코드 구현
static void floydWarshall(){
for(int k=1; k<=N; k++){
for(int i=1; i<=N; i++){
for(int j=1; j<=N; j++){
// k를 거쳐가는 비용이 INF인 경우 못가는 곳이라 의미없음(오버플로우 방지용)
if(dist[i][k] == INF || dist[k][j] == INF){
continue;
}
// i->j 보다 i->k->j가 작으면 갱신
dist[i][j] = Math.min(dist[i][j], dist[i][k] + dist[k][j]);
}
}
}
}
예제 문제
백준 2458번 : 키 순서
https://www.acmicpc.net/problem/2458
[코테] 백준 2458번 : 키 순서 (java)
https://www.acmicpc.net/problem/2458알고리즘 분류 : 그래프 이론, 그래프 탐색, 깊이 우선 탐색, 최단 경로, 플로이드–워셜❓문제🔅해석모든 학생의 키를 비교한 횟수를 알아야하기 때문에 전체 쌍의
steady-record.tistory.com
다익스트라 알고리즘 (Dijkstra's Algorithm)
- 음이 아닌 가중 그래프에서의 단일 쌍, 단일 출발, 단일 도착 최단 경로 문제
- 시작점이 있고, 모든 노드로 최단 거리를 구할 때
- 인접 리스트 사용
- PQ로 최소 cost 뽑으면서 정점을 방문하여 최단 거리 갱신
- 음의 간선이 없으므로 각 노드에 최초 방문 시 최단 거리를 확정한다. (방문 체크 필요)

동작 원리
- 시작 정점 설정
- 시작 정점을 선택하고, 이 정점에서 다른 모든 정점으로의 최단 거리를 저장할 배열을 초기화한다. 시작 정점의 거리는 0으로 설정하고, 나머지 정점의 거리는 무한대로 설정한다.
- 방문하지 않은 정점 중 최단 거리 정점 선택한다.
- 인접한 정점들의 거리 갱신
- 선택한 정점의 인접한 정점들에 대해, 현재 정점을 거쳐 가는 것이 더 짧은 경로라면, 그 경로로 거리를 갱신한다.
- 모든 정점을 방문할 때까지 반복한다.
Node 클래스
정점의 번호와 해당 정점까지의 비용을 포함한다.
Comparable 인터페이스를 구현하여 우선순위 큐에서 최소 비용의 정점이 먼저 나오도록 한다.
static class Node implements Comparable<Node> {
int dest;
int cost;
public Node(int dest, int cost) {
this.dest = dest;
this.cost = cost;
}
@Override
public int compareTo(Node o) {
return Integer.compare(this.cost, o.cost);
}
}
코드 구현
static void dijkstra(int start) {
PriorityQueue<Node> pq = new PriorityQueue<>();
Arrays.fill(dist, Integer.MAX_VALUE);
dist[start] = 0;
// 시작점: 1번 노드
pq.offer(new Node(start, 0));
while (!pq.isEmpty()) {
Node current = pq.poll();
// 목적지 노드가 이미 방문했던 정점이면 다시 방문하지 않는다
// 첫번째 방문에서 최단거리가 결정되기 때문
if (visited[current.dest]) {
continue;
}
// 방문처리
visited[current.dest] = true;
for (Node next : adjList[current.dest]) {
if (dist[next.dest] > next.cost + current.cost) {
dist[next.dest] = next.cost + current.cost;
pq.offer(new Node(next.dest, dist[next.dest]));
}
}
}
}
예제 문제
백준 1753번 : 최단경로
https://www.acmicpc.net/problem/1753
[코테] 백준 1753번 : 최단경로 (java)
https://www.acmicpc.net/problem/1753알고리즘 분류 : 그래프 이론, 데이크스트라, 최단 경로❓문제🔅해석음이 아닌 가중 그래프에서의 단일 쌍, 단일 출발, 단일 도착 최단 경로 문제에서는 다익스트라
steady-record.tistory.com
벨만-포드 알고리즘 (Bellman-Ford Algorithm)
- 가중 그래프에서의 단일 쌍, 단일 출발, 단일 도착 최단 경로 문제
- 음수의 간선을 포함 할 수 있다.
- 음수의 사이클이 존재할 수 있다.
- V-1번 탐색하여 최단 거리를 구하고 V번 구했을 때, 최단거리 갱신이 된다면, 음수의 사이클이 존재한다는 것이다.
- 케이스가 3000 ~ 5000

동작원리
- 거리 초기화
- 시작 정점의 거리를 0으로 설정하고, 나머지 모든 정점의 거리를 무한대로 설정한다.
- 거리 갱신
- 모든 간선에 대해 V-1번 반복해서 간선의 시작 정점에서 도착 정점으로 가는 경로가 현재 알려진 경로보다 짧다면, 그 경로를 갱신한다.
- 음수 사이클 검출
- 모든 간선에 대해 추가로 한 번 더 거리 갱신을 한다. 이 과정에서 최단 거리 갱신이 되면, 음수 사이클이 존재한다고 판단할 수 있다.
Edge 클래스
static class Edge{
int from;
int to;
int cost;
public Edge(int from, int to, int cost){
this.from = from;
this.to = to;
this.cost = cost;
}
}
코드 구현
static boolean bellmanFordMoore(int V, int start){
Arrays.fill(dist, Long.MAX_VALUE);
dist[start] = 0;
// V-1번 E개의 모든 간선 확인
for(int i=0; i<V-1; i++){
for(Edge edge : adjList){
// 간선의 시작점이 아직 탐색 불가면 continue
if(dist[edge.from] == Long.MAX_VALUE){
continue;
}
// 최단거리 갱신
if(dist[edge.to] > dist[edge.from] + edge.cost){
dist[edge.to] = dist[edge.from] + edge.cost;
}
}
}
boolean isNegativeCycle = false;
// V번째 E개의 모든 간선을 확인해서 갱신되는 구간이 있으면 음의 사이클이 존재하는 것
for(Edge edge : adjList){
if(dist[edge.from] == Long.MAX_VALUE){
continue;
}
if(dist[edge.to] > dist[edge.from] + edge.cost){
isNegativeCycle = true;
break;
}
}
return isNegativeCycle;
}
예제 문제
백준 11657번 : 타임 머신
https://www.acmicpc.net/problem/11657
문제 풀이
[코테] 백준 11657번 : 타임 머신 (java)
https://www.acmicpc.net/problem/11657알고리즘 분류 : 그래프 이론, 최단 경로, 벨만–포드❓문제 🔅해석 1. 거리 초기화 시작 정점의 거리를 0으로 설정하고, 나머지 모든 정점의 거리를 무한대
steady-record.tistory.com
플로이드-워셜 알고리즘 (Floyd-Warshall Algorithm)
- 전체 쌍 최단 경로 문제
- 케이스가 300 ~ 500
- 그래프에서 음수 가중치의 간선이 존재할 수 있지만, 음수 사이클(negative cycle)은 없어야 한다.

동작 원리
플로이드-워셜 알고리즘은 동적 프로그래밍(Dynamic Programming)을 기반으로 하며, 점진적으로 모든 정점 간의 최단 경로를 계산한다. 이 알고리즘의 핵심 아이디어는 "중간에 다른 정점을 거치는 경로가 직접 연결된 경로보다 더 짧을 수 있다"는 점이다.
- 거리 초기화
- 그래프의 인접 행렬(Adjacency Matrix)로 초기화한다. 만약 두 정점 간에 직접 연결된 간선이 있다면 그 가중치로 초기화하고, 연결되어 있지 않다면 무한대(또는 매우 큰 값)로 설정한다. 자신에게 가는 거리는 0으로 설정한다.
- 동적 프로그래밍(DP) 적용
- 각 정점을 중간 정점으로 고려하여, 다른 모든 정점 쌍에 대해 최단 경로를 갱신한다. 즉, 정점 k를 중간 정점으로 사용하는 경우, i에서 j로 가는 경로가 i -> k -> j로 더 짧아질 수 있는지 확인하고, 그렇다면 경로를 갱신한다.
- 결과 출력 : 모든 정점 쌍 간의 최단 경로가 담긴 행렬을 출력합니다.
코드 구현
static void floydWarshall(){
for(int k=1; k<=N; k++){
for(int i=1; i<=N; i++){
for(int j=1; j<=N; j++){
// k를 거쳐가는 비용이 INF인 경우 못가는 곳이라 의미없음(오버플로우 방지용)
if(dist[i][k] == INF || dist[k][j] == INF){
continue;
}
// i->j 보다 i->k->j가 작으면 갱신
dist[i][j] = Math.min(dist[i][j], dist[i][k] + dist[k][j]);
}
}
}
}
예제 문제
백준 2458번 : 키 순서
https://www.acmicpc.net/problem/2458
[코테] 백준 2458번 : 키 순서 (java)
https://www.acmicpc.net/problem/2458알고리즘 분류 : 그래프 이론, 그래프 탐색, 깊이 우선 탐색, 최단 경로, 플로이드–워셜❓문제🔅해석모든 학생의 키를 비교한 횟수를 알아야하기 때문에 전체 쌍의
steady-record.tistory.com
