MST (최소 신장 트리)
- Minimum Spanning Tree
- 가중치가 있는 연결 그래프에서 모든 정점을 포함하면서, 간선의 가중치 합이 최소가 되는 트리
- 이를 찾기 위한 대표적인 알고리즘으로 크루스칼 알고리즘과 프림 알고리즘이 있다.
크루스칼 알고리즘(Kruskal's Algorithm)
- 그래프의 모든 간선을 가중치 순으로 정렬한 후, 가중치가 가장 작은 간선부터 선택하여 트리를 구성하는 방법이다.
- 이 과정에서 사이클을 형성하는 간선은 선택하지 않는다.
- 간선 위주, union-find 사용
순서
- 간선 정렬: 그래프의 모든 간선을 가중치 기준으로 오름차순 정렬한다.
- 간선 선택: 정렬된 간선 리스트에서 순차적으로 간선을 선택한다. 이때, 선택된 간선이 사이클을 형성하지 않는다면 해당 간선을 최소 신장 트리에 추가한다.
- 사이클 검증: 사이클이 형성되는지 확인하기 위해서 유니온-파인드(Union-Find) 자료 구조를 사용한다. 두 정점이 이미 같은 집합(연결된 트리)에 속해 있다면, 그 간선을 선택하지 않는다.
- 반복: 모든 정점이 연결될 때까지(즉, 간선의 수가 정점 수 - 1이 될 때까지) 이 과정을 반복한다.
코드 구현
static int kruscal(){
int mstCost = 0;
int selectedEdgeCount = 0;
Arrays.sort(edges);
edgesPrinter();
for(int i=0; i<E; i++){
// from과 to 정점이 서로 다른 트리(=서로 다른 subset에 속함)일때만 연결
if(find(edges[i].from) != find(edges[i].to)){
mstCost += edges[i].cost;
selectedEdgeCount++;
// 같은 subset으로 union
union(edges[i].from, edges[i].to);
System.out.println("[" + i + "] ("+edges[i].from+", "+edges[i].to+") +"+edges[i].cost+" Total:"+ mstCost);
// print selected Edge info
parentPrinter();
}
if(selectedEdgeCount == V-1){
return mstCost;
}
}
// MST 만들기 실패했을 경우(연결 불가능한 정점이 존재)
return -1;
}
// Union-Find
static void initUnionFind(){
parent = new int[V+1];
// init parent
for(int i=1; i<=V; i++){
parent[i] = i;
}
}
static void union(int a, int b){
int aRoot = find(a);
int bRoot = find(b);
if(aRoot != bRoot){
parent[bRoot] = aRoot;
}
}
static int find(int a){
if(parent[a] == a){
return a;
}
// Union-Find 경로압축 예시
return parent[a] = find(parent[a]);
}
시간 복잡도
- 간선 정렬: O(ElogE)
- 유니온 파인드: O(ElogV)
- 총 시간 복잡도: O(ElogE+ElogV)=O(ElogV)
예제 문제
백준 1922번 : 네트워크 연결
https://www.acmicpc.net/problem/1922
[코테] 백준 1922번 : 네트워크 연결 (java)
https://www.acmicpc.net/problem/1922알고리즘 분류 : 그래프 이론, 최소 스패닝 트리❓문제🔅해석컴퓨터 == 정점선 == 간선 모든 컴퓨터(정점)를 연결하여 최소의 비용(가중치)을 얻기 위해 MST를 구현한
steady-record.tistory.com
프림 알고리즘 (Prim's Algorithm)
- 시작 정점에서부터 출발하여 인접한 정점 중 가중치가 가장 작은 간선을 선택하면서 트리를 확장한다.
- 노드 위주, Priority Queue 사용
순서
- 시작 정점(보통 1)을 선택하여 MST에 추가한다.
- 선택된 정점에 인접한 간선들을 우선순위 큐(Priority Queue)에 넣는다.
- 우선순위 큐에서 가장 가중치가 작은 간선을 꺼낸다.
- 해당 간선이 연결하는 두 정점 중에서, 트리에 포함되지 않은 정점을 MST에 추가한다.
- 이때, 이미 트리에 포함된 정점과 연결된 간선은 무시한다.
코드 구현
static int prim(){
int mstCost = 0;
boolean[] selected = new boolean[V+1];
int selectedVertexCount = 0;
PriorityQueue<Edge> pq = new PriorityQueue<>();
// 시작노드를 1번 노드로 세팅함
pq.offer(new Edge(1, 0));
while(!pq.isEmpty()){
Edge currentEdge = pq.poll();
System.out.println("("+currentEdge.to+", "+currentEdge.cost+")");
int nextVertex = currentEdge.to;
// 다음 정점이 이미 선택된 정점이면 스킵
if(selected[nextVertex]){
continue;
}
// 다음 정점 선택
selected[nextVertex] = true;
mstCost += currentEdge.cost;
selectedVertexCount++;
// 모든 정점이 선택되었으면 MST 구성 완료
if(selectedVertexCount == V){
return mstCost;
}
// 다음 정점 = nextVertex = currentEdge.to
// 다음 정점이 출발점인 간선 = edge
for(Edge edge : adjList[nextVertex]){
// edge의 목적지 노드가 선택되지 않은 노드면 해당 간선을 pq에 넣음
if(!selected[edge.to]){
pq.offer(edge);
}
}
}
// MST 만들기 실패했을 경우(연결 불가능한 정점이 존재)
return -1;
}
시간 복잡도
- 우선순위 큐(Priority Queue)를 이용할 경우: O(ElogV)
LCA (최소 공통 조상)
- Lowest Common Ancestor
- 두 노드의 가장 가까운 공통 조상을 찾는 문제
LCA의 기본 개념
트리에서 두 노드 A와 B가 있을 때, A와 B의 공통 조상 중에서 가장 깊이 있는 조상을 LCA라고 한다.
예를 들어, 다음과 같은 트리 구조가 있다고 가정한다.
1
/ \
2 3
/ \ \
4 5 6
/ \
7 8
이 트리에서 노드 7과 8의 LCA는 4이고, 노드 4와 6의 LCA는 1이다.
Sparse table 를 이용한 LCA를 구하는 방법
1. BFS로 트리 탐색
bfs로 트리를 탐색하면서 각 노드의 깊이(depth)와 부모(parent)를 기록한다.
이를 통해 각 노드의 깊이를 알 수 있고, 부모를 통해 상위 노드로 이동할 수 있다.
static void bfs(int root){
ArrayDeque<Integer> queue = new ArrayDeque<>();
// root: 1번 노드로 정함
queue.add(root);
depth[root] = 0;
visited[root] = true;
while(!queue.isEmpty()) {
int currentNode = queue.poll();
for (int nextNode : adjList[currentNode]) {
if(!visited[nextNode]){
visited[nextNode] = true;
parent[0][nextNode] = currentNode;
depth[nextNode] = depth[currentNode] + 1;
queue.add(nextNode);
}
}
}
}
2. 희소 테이블(Sparse Table) 구성
각 노드에 대해 2^k번째 부모를 미리 계산한다. 이 테이블을 이용하면, 두 노드의 깊이를 맞춘 후, 공통 조상을 빠르게 찾을 수 있다.
static void findAncestors(){
for(int k=1; k<=LOG; k++){
for(int v=1; v<=N; v++){
parent[k][v] = parent[k-1][parent[k-1][v]];
}
}
}
3. LCA 질의 처리
두 노드의 깊이가 다르면, 깊이가 깊은 노드를 위로 끌어올려 깊이를 맞춘 후, 공통 조상을 찾아간다. 이 과정에서 희소 테이블을 이용하면, 각 단계에서 효율적으로 부모를 탐색할 수 있다.
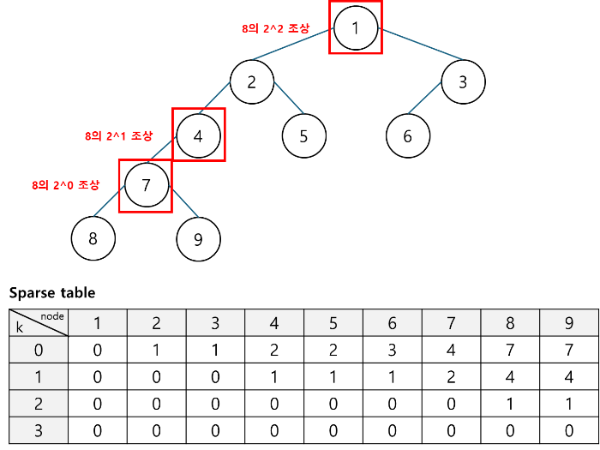
예제 문제
백준 11438번 : LCA 2
https://www.acmicpc.net/problem/11438
[코테] 백준 11438번 : LCA 2 (java)
https://www.acmicpc.net/problem/11438알고리즘 분류 : 자료 구조, 트리, 최소 공통 조상, 희소 배열❓문제🔅해석순서 input된 값을 adjacent list(양방향 간선)에 넣는다.BFS로 트리 탐색bfs로 트리를 탐색하
steady-record.tistory.com
MST (최소 신장 트리)
- Minimum Spanning Tree
- 가중치가 있는 연결 그래프에서 모든 정점을 포함하면서, 간선의 가중치 합이 최소가 되는 트리
- 이를 찾기 위한 대표적인 알고리즘으로 크루스칼 알고리즘과 프림 알고리즘이 있다.
크루스칼 알고리즘(Kruskal's Algorithm)
- 그래프의 모든 간선을 가중치 순으로 정렬한 후, 가중치가 가장 작은 간선부터 선택하여 트리를 구성하는 방법이다.
- 이 과정에서 사이클을 형성하는 간선은 선택하지 않는다.
- 간선 위주, union-find 사용
순서
- 간선 정렬: 그래프의 모든 간선을 가중치 기준으로 오름차순 정렬한다.
- 간선 선택: 정렬된 간선 리스트에서 순차적으로 간선을 선택한다. 이때, 선택된 간선이 사이클을 형성하지 않는다면 해당 간선을 최소 신장 트리에 추가한다.
- 사이클 검증: 사이클이 형성되는지 확인하기 위해서 유니온-파인드(Union-Find) 자료 구조를 사용한다. 두 정점이 이미 같은 집합(연결된 트리)에 속해 있다면, 그 간선을 선택하지 않는다.
- 반복: 모든 정점이 연결될 때까지(즉, 간선의 수가 정점 수 - 1이 될 때까지) 이 과정을 반복한다.
코드 구현
static int kruscal(){
int mstCost = 0;
int selectedEdgeCount = 0;
Arrays.sort(edges);
edgesPrinter();
for(int i=0; i<E; i++){
// from과 to 정점이 서로 다른 트리(=서로 다른 subset에 속함)일때만 연결
if(find(edges[i].from) != find(edges[i].to)){
mstCost += edges[i].cost;
selectedEdgeCount++;
// 같은 subset으로 union
union(edges[i].from, edges[i].to);
System.out.println("[" + i + "] ("+edges[i].from+", "+edges[i].to+") +"+edges[i].cost+" Total:"+ mstCost);
// print selected Edge info
parentPrinter();
}
if(selectedEdgeCount == V-1){
return mstCost;
}
}
// MST 만들기 실패했을 경우(연결 불가능한 정점이 존재)
return -1;
}
// Union-Find
static void initUnionFind(){
parent = new int[V+1];
// init parent
for(int i=1; i<=V; i++){
parent[i] = i;
}
}
static void union(int a, int b){
int aRoot = find(a);
int bRoot = find(b);
if(aRoot != bRoot){
parent[bRoot] = aRoot;
}
}
static int find(int a){
if(parent[a] == a){
return a;
}
// Union-Find 경로압축 예시
return parent[a] = find(parent[a]);
}
시간 복잡도
- 간선 정렬: O(ElogE)
- 유니온 파인드: O(ElogV)
- 총 시간 복잡도: O(ElogE+ElogV)=O(ElogV)
예제 문제
백준 1922번 : 네트워크 연결
https://www.acmicpc.net/problem/1922
[코테] 백준 1922번 : 네트워크 연결 (java)
https://www.acmicpc.net/problem/1922알고리즘 분류 : 그래프 이론, 최소 스패닝 트리❓문제🔅해석컴퓨터 == 정점선 == 간선 모든 컴퓨터(정점)를 연결하여 최소의 비용(가중치)을 얻기 위해 MST를 구현한
steady-record.tistory.com
프림 알고리즘 (Prim's Algorithm)
- 시작 정점에서부터 출발하여 인접한 정점 중 가중치가 가장 작은 간선을 선택하면서 트리를 확장한다.
- 노드 위주, Priority Queue 사용
순서
- 시작 정점(보통 1)을 선택하여 MST에 추가한다.
- 선택된 정점에 인접한 간선들을 우선순위 큐(Priority Queue)에 넣는다.
- 우선순위 큐에서 가장 가중치가 작은 간선을 꺼낸다.
- 해당 간선이 연결하는 두 정점 중에서, 트리에 포함되지 않은 정점을 MST에 추가한다.
- 이때, 이미 트리에 포함된 정점과 연결된 간선은 무시한다.
코드 구현
static int prim(){
int mstCost = 0;
boolean[] selected = new boolean[V+1];
int selectedVertexCount = 0;
PriorityQueue<Edge> pq = new PriorityQueue<>();
// 시작노드를 1번 노드로 세팅함
pq.offer(new Edge(1, 0));
while(!pq.isEmpty()){
Edge currentEdge = pq.poll();
System.out.println("("+currentEdge.to+", "+currentEdge.cost+")");
int nextVertex = currentEdge.to;
// 다음 정점이 이미 선택된 정점이면 스킵
if(selected[nextVertex]){
continue;
}
// 다음 정점 선택
selected[nextVertex] = true;
mstCost += currentEdge.cost;
selectedVertexCount++;
// 모든 정점이 선택되었으면 MST 구성 완료
if(selectedVertexCount == V){
return mstCost;
}
// 다음 정점 = nextVertex = currentEdge.to
// 다음 정점이 출발점인 간선 = edge
for(Edge edge : adjList[nextVertex]){
// edge의 목적지 노드가 선택되지 않은 노드면 해당 간선을 pq에 넣음
if(!selected[edge.to]){
pq.offer(edge);
}
}
}
// MST 만들기 실패했을 경우(연결 불가능한 정점이 존재)
return -1;
}
시간 복잡도
- 우선순위 큐(Priority Queue)를 이용할 경우: O(ElogV)
LCA (최소 공통 조상)
- Lowest Common Ancestor
- 두 노드의 가장 가까운 공통 조상을 찾는 문제
LCA의 기본 개념
트리에서 두 노드 A와 B가 있을 때, A와 B의 공통 조상 중에서 가장 깊이 있는 조상을 LCA라고 한다.
예를 들어, 다음과 같은 트리 구조가 있다고 가정한다.
1
/ \
2 3
/ \ \
4 5 6
/ \
7 8
이 트리에서 노드 7과 8의 LCA는 4이고, 노드 4와 6의 LCA는 1이다.
Sparse table 를 이용한 LCA를 구하는 방법
1. BFS로 트리 탐색
bfs로 트리를 탐색하면서 각 노드의 깊이(depth)와 부모(parent)를 기록한다.
이를 통해 각 노드의 깊이를 알 수 있고, 부모를 통해 상위 노드로 이동할 수 있다.
static void bfs(int root){
ArrayDeque<Integer> queue = new ArrayDeque<>();
// root: 1번 노드로 정함
queue.add(root);
depth[root] = 0;
visited[root] = true;
while(!queue.isEmpty()) {
int currentNode = queue.poll();
for (int nextNode : adjList[currentNode]) {
if(!visited[nextNode]){
visited[nextNode] = true;
parent[0][nextNode] = currentNode;
depth[nextNode] = depth[currentNode] + 1;
queue.add(nextNode);
}
}
}
}
2. 희소 테이블(Sparse Table) 구성
각 노드에 대해 2^k번째 부모를 미리 계산한다. 이 테이블을 이용하면, 두 노드의 깊이를 맞춘 후, 공통 조상을 빠르게 찾을 수 있다.
static void findAncestors(){
for(int k=1; k<=LOG; k++){
for(int v=1; v<=N; v++){
parent[k][v] = parent[k-1][parent[k-1][v]];
}
}
}
3. LCA 질의 처리
두 노드의 깊이가 다르면, 깊이가 깊은 노드를 위로 끌어올려 깊이를 맞춘 후, 공통 조상을 찾아간다. 이 과정에서 희소 테이블을 이용하면, 각 단계에서 효율적으로 부모를 탐색할 수 있다.

예제 문제
백준 11438번 : LCA 2
https://www.acmicpc.net/problem/11438
[코테] 백준 11438번 : LCA 2 (java)
https://www.acmicpc.net/problem/11438알고리즘 분류 : 자료 구조, 트리, 최소 공통 조상, 희소 배열❓문제🔅해석순서 input된 값을 adjacent list(양방향 간선)에 넣는다.BFS로 트리 탐색bfs로 트리를 탐색하
steady-record.tistory.com
