[삼성SDS] 24년 하반기 대학생 알고리즘 특강(Day6) : 그래프(서로소 집합(Union-Find), 위상정렬(Topological Sort))

그래프 (Graph)

• 현실세계의 사물이나 개념 간의 연결 관계를 수학적 모델로 단순화하여 표현한 것

 

그래프 표현

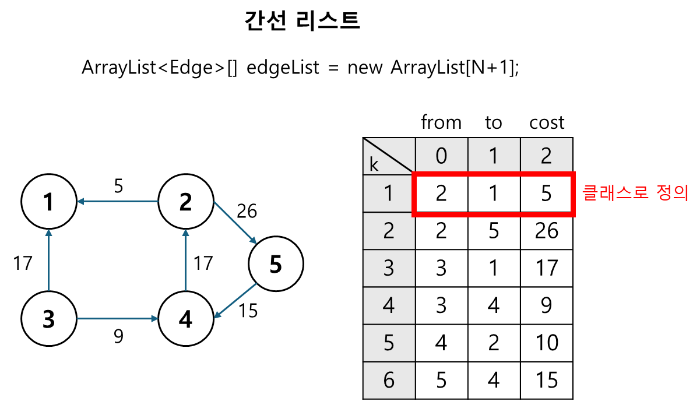
1. 간선 리스트(Edge List)

• 정점의 개수가 V개, 간선의 개수가 E개인 그래프에 대해서 E x 2 (or E x 3) 이차원 배열(A)에 간선 정보를 저장
• 어떤 두 정점 vi, vj를 연결하는 간선 ek = (vi, vj) 에 대해서 A[k][0] = vi, A[k][1] = vi
• 가중치 그래프의 경우 배열의 3번째 열에 간선의 가중치를 저장
• 벨만-포드 알고리즘에서 사용한다.

그래프 표현 - 간선 리스트

코드 구현

간선 정보 class

static class Edge{
    int from;
    int to;
    int cost;

    public Edge(int from, int to, int cost){
        this.from = from;
        this.to = to;
        this.cost = cost;
    }
}

 

인접 리스트 생성

ArrayList<Edge>[] edgeList = new ArrayList[N+1];
// 각 정점별 인접리스트 init
for(int n=0; n<N+1; n++){
    edgeList[n] = new ArrayList<>();
}

int from, to, cost;
for(int m=0; m<M; m++){
    st = new StringTokenizer(br.readLine());
    from = Integer.parseInt(st.nextToken());
    to = Integer.parseInt(st.nextToken());
    cost = Integer.parseInt(st.nextToken());

    edgeList[from].add(new Edge(from, to, cost));
}

 

 

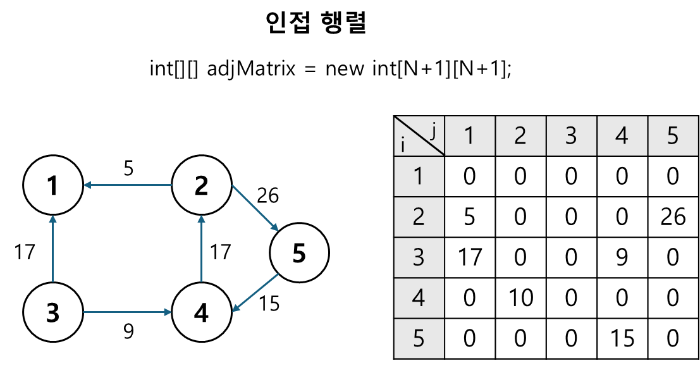
2. 인접 행렬(Adjacency Matrix)

• 정점의 개수가 V개, 간선의 개수가 E개인 그래프에 대해서 V x V 이차원 배열(A)에 그래프 정보를 저장
• 플로이드-워셜 알고리즘에서 사용한다.

그래프 표현 - 인접 행렬

코드 구현

int[][] adjMatrix = new int[N+1][N+1];

int from, to, cost;
for(int m=0; m<M; m++){
    st = new StringTokenizer(br.readLine());
    from = Integer.parseInt(st.nextToken());
    to = Integer.parseInt(st.nextToken());
    cost = Integer.parseInt(st.nextToken());

    adjMatrix[from][to] = cost;
}

 

 

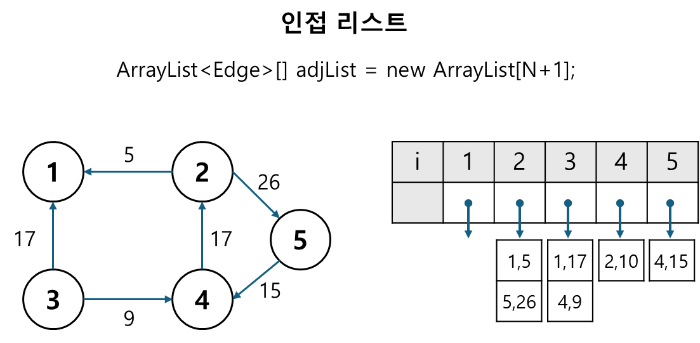
3. 인접 리스트 (Adjacent List)

• 정점의 개수가 V개, 간선의 개수가 E개인 그래프에 대해서 V개의 연결 리스트로 그래프 정보를 저장
• 다익스트라 알고리즘에서 사용한다.

그래프 표현 - 인접 리스트

코드 구현

간선 정보 class

public static class Edge{
    int node;
    int cost;

    public Edge(int node, int cost){
        this.node = node;
        this.cost = cost;
    }
}

 

인접 리스트 생성

ArrayList<Edge>[] adjList = new ArrayList[N+1];
// 각 정점별 인접리스트 init
for(int n=0; n<N+1; n++){
    adjList[n] = new ArrayList<>();
}

int from, to, cost;
for(int m=0; m<M; m++){
    st = new StringTokenizer(br.readLine());
    from = Integer.parseInt(st.nextToken());
    to = Integer.parseInt(st.nextToken());
    cost = Integer.parseInt(st.nextToken());

    adjList[from].add(new Edge(to, cost));
}

 

 

---

서로소 집합(Union-Find)

• Disjoint Set
• 교집합이 공집합인 집합(서로소 집합)들의 정보를 확인(Find)하고 조작(Union)할 수 있는 자료구조
• Union 연산
  • 어떤 두 원소 a, b에 대해서 각 원소가 속한 집합을 하나로 합치는 연산
  • a, b의 부모가 다르면 두 원소는 같은 집합에 속해 있지 않다. a의 부모를 b의 부모로 대입 or b의 부모를 a의 부모로 대입하여 하나로 합친다.
• Find 연산
  • 어떤 원소 a에 대해서 a가 속한 집합(집합의 대표번호)을 반환

 

 

 

 

코드 구현

- union

private static void union(int a, int b) {
    int aRoot = find(a);
    int bRoot = find(b);
    if (aRoot != bRoot)
        parent[aRoot] = bRoot;

}

 

 

- find

private static int find(int a) {
    if (parent[a] == a)
        return a;
    return parent[a] = find(parent[a]);
}

 

 

예제문제

https://www.acmicpc.net/problem/1717

백준 1717번 : 집합의 표현

기본적인 union-find 문제이다.

 

자세한 풀이는 아래 링크를 참고해주세요.

[코테] 백준 1717번 : 집합의 표현 (java)

 

 

---

위상정렬(Topological Sort)

• DAG (비순환 방향 그래프)
  
  • 순환을 가지지 않는 방향 그래프
  • 일반적으로 우선순위(선행작업 후 후행작업)를 가진 일련의 작업들은 DAG 구조를 가진다.
• 위상정렬
  
  • DAG에서 그래프의 방향성을 거스르지 않고 정점들을 나열하는 것
  • 일반적으로 위상정렬의 결과는 유일하지 않다.
  • 교과 과정 설계, 작업 스케줄링, 컴파일러의 코드 컴파일 순서 등에 활용된다.

 

순서

1. 입력시 indegree[] 를 계산한다. (indegree : 해당 노드를 향해 들어오는 간선의 개수)
2. bfs처럼 Queue를 사용하여 indegree 배열 중에서 0인 노드를 처리한다.

1. indegree 계산 및 indegree 배열 중에서 0인 노드를 Queue에 담는다.

 

 

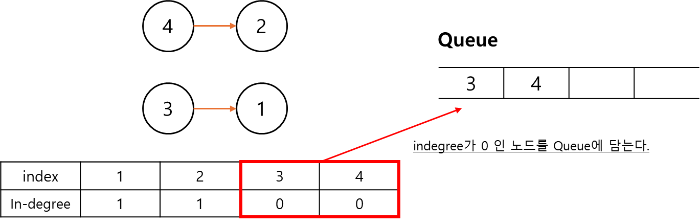
2. Queue에서 pop를 하고, 3(pop 한 값)과 연결된 노드에 indegree를 하나 감소시킨다.

 

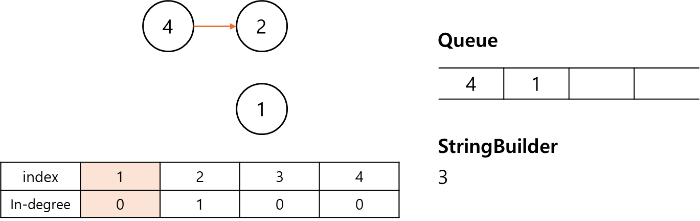
3. 모든 노드의 indegree가 0이 될 때 까지 반복한다.

 

 

예제 문제

https://www.acmicpc.net/problem/2252

백준 2252번 : 줄 세우기

 

[코테] 백준 2252번 : 줄 세우기 (java)