정렬
- 정렬을 통해 유일성 검사 및 중복 제거가 가능하다.
- 정렬된 데이터를 한번씩만 확인하면 각 숫자의 빈도 수를 확인할 수 있다.
정렬 방법
1. Arrays.sort()
- 오름차순
int[] arr = {5, 3, 2, 8, 1};
Arrays.sort(arr);
System.out.println(Arrays.toString(arr)); // [1, 2, 3, 5, 8]
- 내림차순
Arrays.sort(arr, Comparator.reverseOrder());
System.out.println(Arrays.toString(arr)); // [8, 5, 3, 2, 1]
2. 사용자 정의 정렬 (Comparator)
Integer[] arr = {5, 3, 2, 8, 1};
Arrays.sort(arr, new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o1 - o2; //오름차순
//return o2 - o1; //내림차순
}
})
System.out.println(Arrays.toString(arr)); // [1, 2, 3, 5, 8]
return 값이 음수 or 0 이면 두 데이터를 바꾸지 않는다. 양수이면 두 데이터를 바꾼다.
첫번째 숫자(o1)에서 두번째 숫자(o2)를 뺏을 때,
음수가 나오면 오름차순,
양수가 나오면 o1이 더 크니깐 내림차순으로 된다고 생각한다.
3. 람다식
Arrays.sort(arr, (o1, o2) -> o1 - o2); //오름차순
Arrays.sort(arr, (o1, o2) -> o2 - o1); //내림차순
4. 객체 Comparable
- 클래스에 대해 정렬하는 방법이다.
- Comparable로 기본 정렬을 넣어주고 추가 정렬이 필요하다면 compartor를 사용한다.
class Item implements Comparable<Item> {
private String name;
private int price;
public Item(String name, int price) {
this.name = name;
this.price = price;
}
public String getName() {
return name;
}
public int getPrice() {
return price;
}
@Override
public int compareTo(Item other) {
int resultPrice = price - other.weight;
if (resultPrice == 0) {
return other.value - value;
}
return resultPrice;
}
@Override
public String toString() {
return "Item{name='" + name + "', price=" + price + '}';
}
}
정렬 조건을 2개 이상 쓸 수도 있다.
먼저 가격을 오름차순으로 정렬하고 만약 가격이 같다면 제품명을 내림차순으로 정렬한다.
import java.util.Arrays;
public static void main(String[] args) {
Item[] items = {
new Item("Item1", 50),
new Item("Item2", 30),
new Item("Item3", 20)
};
Arrays.sort(items);
System.out.println(Arrays.toString(items));
// Output: [Item{name='Item5', price=10}, Item{name='Item3', price=20}, Item{name='Item2', price=30}]
}
5. Comparator.comparing 함수
- 4번과 같이 객체를 정렬한다고 했을 때 사용한다.
- Comparator.comparing(클래스::getter)
- 클래스 안에 getter가 존재해야 한다.
- thenComparing 으로 덧붙일 수 있다.
- 오름차순
Arrays.sort(items, Comparator.comparing(Item::getPrice));
Arrays.sort(items, Comparator.comparing(Item::getPrice).thenComparing(Item::getName);
- 내림차순
Arrays.sort(items, Comparator.comparing(Item::getPrice).reversed());
6. Stream API를 이용한 정렬
- Java 8부터는 Stream API를 이용하여 컬렉션을 정렬할 수 있다.
List<String> list = new ArrayList<>(Arrays.asList("banana", "apple", "cherry"));
List<String> sortedList = list.stream().sorted().collect(Collectors.toList());
System.out.println(sortedList); // [apple, banana, cherry]
예제 문제
백준 1713번 : 후보 추천하기
https://www.acmicpc.net/problem/1713
학생을 객체로 만들어 조건에 맞게 정렬을 한다.
단, ArrayList 특성을 이해하여 오름차순으로 정렬할 지, 내림차순으로 정렬할지 잘 생각해야한다.
자세한 풀이는 아래 링크를 참고해주세요.
[코테] 백준 1713번 : 후보 추천하기
https://www.acmicpc.net/problem/1713알고리즘 분류 : 구현, 시뮬레이션❓문제🔅해석학생 객체에 학생 번호, 추천 수, 타임스탬프를 저장하여 조건에 맞게 정렬을 한다. Student[] students = new Student[101]; //학
steady-record.tistory.com
투 포인터
- 배열이나 리스트와 같은 데이터 구조에서 두 개의 포인터를 사용하여 특정 문제를 효율적으로 해결하는 방법이다.
- 주로 정렬된 배열에서 부분 배열을 찾거나, 특정 조건을 만족하는 연속된 부분을 찾을 때 사용된다.
예제 문제
백준 2003번 : 수들의 합 2
입력받은 배열에 low pointer와 high pointer가 하나씩 증가하면서 합의 조합을 찾는다.
이 때, high를 증가하면 전체 합이 증가하고, low를 증가하면 전체 합이 감소된다.
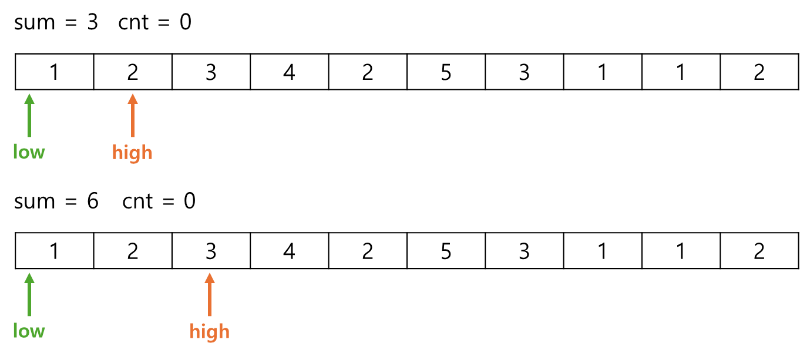
자세한 풀이는 아래 링크를 참고해주세요.
시간복잡도
- 알고리즘의 실행 시간이 입력 크기에 따라 어떻게 증가하는지를 나타내는 중요한 개념이다.
- 시간복잡도를 표기하는 방법에는 빅-오, 빅-오메가, 세타 표기법 등 다양한 방법이 있다.
- 빅-오(Big-Oh, O(N)) : Worst Case의 연산 횟수를 나타냄
- 빅-오메가(Big-Omega, Ω(N)) : Best Case 연산 횟수를 나타냄
- 빅-세타(Big-Theta, θ(N)) : Average Case 연산 횟수를 나타냄
- 일반적으로 시간복잡도를 표현할 땐 빅-오 표기법을 사용한다.
- 빅-오 표기법은 최고차항의 차수만을 표기하는 표기법으로써, 연산 횟수가 3N^2이면 O(N^2)으로 표기한다.
예시
1. 이중 for문
public class NestedForLoop {
public static void main(String[] args) {
int n = 5; // 예를 들어, n이 5라고 가정합니다.
for (int i = 0; i < n; i++) { // 바깥쪽 for문: n번 반복
for (int j = 0; j < n; j++) { // 안쪽 for문: n번 반복
System.out.println("i: " + i + ", j: " + j);
}
}
}
}
이 예제에서 바깥쪽 for문은 n번 반복되고, 그 안쪽 for문도 n번 반복됩니다. 따라서 전체적으로 n * n = n^2번의 반복이 발생합니다.
시간복잡도 : O(N^2)
2. 탈출문이 있는 for문
public class FindElement {
public static void main(String[] args) {
int[] arr = {1, 2, 3, 4, 5};
int target = 3;
for (int i = 0; i < arr.length; i++) {
if (arr[i] == target) {
System.out.println("Element found at index: " + i);
break; // 탈출문
}
}
}
}
최악의 경우 배열의 끝까지 탐색해야 하므로 시간 복잡도는 O(n)이다.
3. 재귀호출
1) 피보나치 수열
public class Fibonacci {
public static void main(String[] args) {
int n = 10; // 예를 들어, n이 10이라고 가정합니다.
System.out.println(fib(n));
}
public static int fib(int n) {
if (n <= 1) {
return n;
}
return fib(n - 1) + fib(n - 2);
}
}
위 코드에서, fib(n)은 fib(n-1)과 fib(n-2)를 각각 한 번씩 호출한다.
트리의 높이는 n에 비례하고, 각 노드가 두 개의 하위 문제로 분할되므로, 호출 횟수는 대략 2^n에 비례한다.
시간복잡도 : O(2^N)
2) 팩토리얼
public class Factorial {
public static void main(String[] args) {
int n = 5;
System.out.println(factorial(n));
}
public static int factorial(int n) {
if (n <= 1) {
return 1;
}
return n * factorial(n - 1);
}
}
팩토리얼 함수 factorial(n)은 factorial(n-1)을 한 번만 호출하여 호출 횟수는 n에 비례한다.
시간복잡도 : O(N)
4. 이진 탐색
public class BinarySearchExample {
public static void main(String[] args) {
int[] arr = {1, 2, 3, 4, 5, 6, 7, 8, 9};
int target = 5;
System.out.println(binarySearch(arr, target)); // true
}
public static boolean binarySearch(int[] arr, int target) {
int left = 0;
int right = arr.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (arr[mid] == target) {
return true;
}
if (arr[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return false;
}
}
매 반복마다 검색 범위를 절반으로 줄인다. 배열의 길이가 N일 때, 최대 비교 횟수는 log2(N)이 된다.
시간복잡도 : O(logN)
시간복잡도의 종류
- O(1) - 상수 시간(Constant Time): 입력 크기에 상관없이 일정한 시간이 걸린다.
- O(log n) - 로그 시간(Logarithmic Time): N개의 정렬된 수열에서 이분탐색을 통해 특정 숫자를 탐색.
- O(n) - 선형 시간(Linear Time): 정렬되지 않은 길이가 N인 배열에서 가장 작은 수를 탐색
- O(n log n) - 선형 로그 시간(Linearithmic Time): 예: 효율적인 정렬 알고리즘(병합 정렬, 퀵 정렬).
- O(n^2) - 이차 시간(Quadratic Time): 입력 크기의 제곱에 비례하여 시간이 증가합니다. 예: 버블 정렬, 삽입 정렬.
- O(2^n) - 지수 시간(Exponential Time): 번호가 매겨진 N개의 동전을 던졌을 때 나올 수 있는 경우를 출력하는 경우. 예: 피보나치 수열의 비효율적 재귀적 구현.
- O(n!) - 팩토리얼 시간(Factorial Time): 1부터 N까지의 숫자를 나열할 수 있는 모든 방법을 출력하는 경우. 예: 외판원 문제의 브루트 포스 해결법.
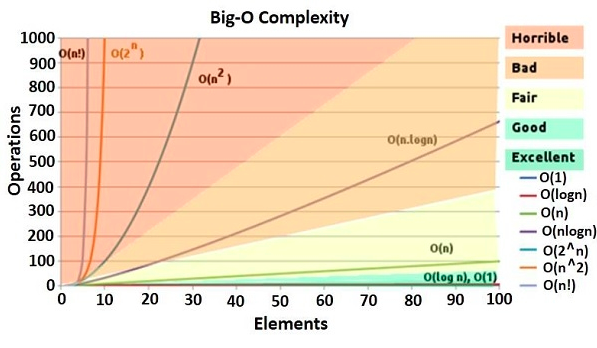
되도록 O(n!), O(2^N), O(N^2)의 시간복잡도가 나오는 것은 피하자.
O(NlogN) 정도도 괜찮지만 줄일 수 있으면 줄인다.
